Using Solver

Understanding Solver

First, since Solver is an Excel add-in, you should make sure that it is enabled. To do this click the Data tab. If Solver is enabled, you will see it on the Data tab:

In order to use Solver, you must set up the worksheet correctly. This requires a

solid understanding of the problem you are trying to solve. The following example involves a business that assembles and sells furniture. The business sells two types of tables: one made from maple and another made from mahogany. The maple table is of lower quality than the other table, but the price is reasonable. The mahogany table is of higher quality and is made from more expensive wood, and so it has a higher price.

From the worksheet, you can see that it takes three hours of rough carpentry to assemble the maple table and four hours of rough carpentry to assemble the mahogany table. Once the table is assembled, it takes one hour of finish work for the maple table and two hours of finish work for the mahogany table.


The goal is to find out how many of each type of table we should make to maximize our weekly total revenue and what the maximum total revenue would be. To complicate matters, the business employs one part-time finish carpenter who is only available for 30 hours of finish work per week, and two rough carpenters that are available for a combined 80 hours of rough carpentry a week. Also, the lumber yard that supplies the business with mahogany can only supply enough for 10 tables a week.


This means that the total finish work hours used must be less than or equal to 30 hours for the week, and the total rough work must be less than or equal to 80 hours. Furthermore, the number of mahogany tables we can make in a week must be less than or equal to 10. These constitute the constraints of the problem.
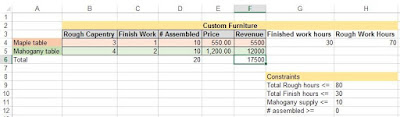
The following worksheet is the same as the previous one, except that the cell formulas are now visible. Examine the cell references in the formulas carefully.

Cells B4 and C4 hold the number of rough carpentry and finish work hours required to build a maple (less expensive) table. Similarly, cells B5 and C5 contain the number of rough work and finish work hours required to assemble a mahogany table. The revenues from the maple tables can be calculated by multiplying the number of tables assembled by the sale price. This is what the formula in F4 does. The revenues from the mahogany tables are calculated by a similar formula in cell F5.

Notice that in both cases, the revenue formulas depend on the number of tables assembled (cells D4 and D5). Because of this, the total revenue formula (F6) is indirectly dependent on D4 and D5.

The formula we want to optimize (also known as the objective formula) represents the total revenue (F6). The cells we will change to maximize the total revenue formula represent the quantities of each type of table assembled (D4 for maple and D5 for mahogany).

The constraints for this problem are shown in the lower right area. It is not absolutely necessary to label the constraints as they are shown here, but clearly identifying them on the worksheet helps when entering the constraints in Solver. We have specified that:

• The rough work hours are to be less than or equal to 80.
• The finish work hours are to be less than or equal to 30'
• The number of mahogany tables that can be assembled is less than or equal to 10.
• The number of each type of table assembled has to be greater than or equal to 0

This last constraint may seem obvious and silly, but it is important to include it so the Solver knows that using negative values in the changing cells is not an option when optimizing the objective formula.

The formulas that calculate the total finish-work hours and rough-work hours used are in cells G4 and H4 respectively. You should notice that these formulas are also dependent on the number of each type of table assembled.

To summarize, in order to use Solver you must have a formula to optimize (called the objective formula) and you must have cells that can be changed to optimize the objective. The cells to be changed should be precedents to the objective formula; that is, the calculation of the objective formula should depend on results in the cells to be changed. If constraints are involved, the formulas to be subjected to the constraints should also be dependent on the changing cells.

In the preceding worksheet, you can see that cells G4 and H4 contain formulas that will be subject to the constraints. Cell F6 contains the objective formula and cells D4 and D5 are the changing cells (the numbers of each type of table that will be made). You should notice that the formulas in cells G4, H4, and F6, are all dependent on the changing cells (either directly or indirectly).

Note: It is assumed throughout that there is enough demand to ensure that every table that is made will be sold. 

To use Solver, click Data → Solver: 

This will invoke the Solver Parameters dialog:

Place your cursor in the “Set Objective” text box and click on the worksheet cell that contains your objective formula (cell F6 from the preceding worksheet).

Since we want to find the maximum total revenue, select the “Max” radio button in the dialog.

To enter the changing cells, place your cursor in the text area under the “By Changing Variable Cells” heading, and select the appropriate cells from the worksheet. For the problem shown here, the changing cells are D4 and D5.

At this stage, the Solver dialog should look like this:

The next step is to add the constraints by clicking the Add button to the right of the large white Constraints area. This will display the Add Constraint box:

To add the first constraint, place the cursor in the Cell Reference box and select the cell with the formula you want to constrain. In this particular example, cell G4 is selected, which contains the formula for calculating the total finish work used. Next, click in the Constraint

box and click the cell that contains the appropriate constraint value. Here, we chose cell H10, which contains the value 30. Next, use the drop-down list in the center to specify the type of relationship required between the two cells. In this case, the constraint reads G4 <= H10; that is, total finish work hours should be less than or equal to 30.

Click OK to enter the constraint and close the Add Constraint dialog. The Solver Parameters dialog now looks like this:

Next, we will follow the same process to enter the cell references for the rest of the constraints:

• Total rough work hours less than or equal to 80: (H4 <= H9)
• Number of mahogany tables less than or equal to 10: (D5 <= H11)
• Number of mahogany tables greater or equal to 0: (D5 >= H12)
• Number of maple tables greater or equal to 0: (D4 >= H12)

Here is the resulting Solver Parameters dialog:

Here is the original worksheet with formulas shown:

Examine the worksheet carefully so that you understand the relationships between the objective, the changing cells, and the constraints as specified in the Solver Parameters dialog.

To implement the Solver, click the Solve button at the bottom of the dialog.

You will now see the Solver Results box:

If the Solver Results dialog reports that a solution has been found, the values that maximize the total profit (the solution) will now be visible in the changing cells in the worksheet (D4 and D5). Moreover, the value of the maximum profit will now be visible in the target cell (F6). The “Keep Solver Solution” radio button will be selected by default. If you click OK, the new (optimum) values will remain in the worksheet.

If you select the “Restore Original Values” radio button and click OK, the solutions that the Solver found will not be entered into the worksheet and the original values will be retained.

The following image shows the worksheet after the Solver solution has been implemented. If 10 maple tables and 10 mahogany tables are assembled, the total revenue will be maximized at 17500.

Generating Reports and Scenarios with Solver

In the Solver Results dialog, you also have the option to save the results as a scenario that you can name and reload into the worksheet at a later date. To do this, click the Save Scenario button in the Solver Results dialog.

You can also select one or more report types from the list at the right of the Solver Results dialog. Just click on a report type to select it and Excel will generate it for you. These formatted reports will be generated on separate worksheets.

Now let’s look at a Limits report based on the Solver solution. (It is generated on a separate worksheet if you select Limits from the report list in the Solver Results dialog before you click OK.) Here is what the report looks like for this case:

Changing Solver Values

Next, let’s look at a Solver solution if some of the factors in the situation were to change.

Here we changed the price for the maple tables from 550 dollars to 750 dollars. Since we have not yet closed Excel or used Solver on another set of data and constraints, when we invoke the Solver Parameters dialog, it will be populated with the same cell references and constraints as before.

When we run the Solver with the new price for a maple table entered into the worksheet, the Solver finds a new solution to maximize profits.

This time, we should assemble 20 maple tables and 5 mahogany tables, for a total revenue of 21000 dollars.

Managing Solver Constraints

Let’s have a look at a few more details about using Solver. In the Solver Parameters dialog, you will see a series of buttons next to the Constraints area:

Here is what each command does.

• If you want to add a new constraint, click Add. 
• If you want to change a constraint, select it and click Change. 
• If you want to delete a constraint, select it and click Delete. 
• Reset All will clear all of the constraints, variables, and options in the Solver Parameters dialog
• Load/Save allows save or load existing problem model.

Using Solver as a Goal Seek Tool

• Finally, you can also use Solver as a kind of advanced goal-seek tool. As an example, have a look at the following worksheet with formulas displayed.

Suppose you want to adjust the number of units sold, the price per unit, and the labor costs so that we generate a profit of $1000. How would you do this?

One way to solve this problem is by using the Solver as a goal seek tool.

1. To begin, you just display the Solver Parameters dialog in the usual way (Data → Solver): 
   
2. In the Solver Parameters dialog, we can simply choose cell B9 (total profit) as the objective, and then click to select the “Value of” radio button rather than Max or Min.
3. The next step is to set the value we are after; we will enter 2000 into the text box to the right of the “Value of” radio button. 
4. The final step is to enter the cells that we want to change to reach our objective. In this example, the cells are B2 (units sold), B4 (price per unit), and B7 (labor costs). We can enter these cells into the “By Changing Variable Cells” text box by typing the references directly or clicking in the worksheet to select the cells.
5. Once everything is ready, it is only a matter of clicking the Solve button in the dialog to find a solution.

When Excel finds a solution, the Solver Results dialog will appear and the solution values will be visible in the worksheet. As before, you can choose to keep the solution values, save them as a scenario, or restore the original values.